برای یافتن مرتبه اجرایی یک تابع چند جمله ای به مرتبه اجرای یعنی بزرگترین توان نگاه میکنیم و آن جواب خواهد بود.

مثال: 

 

f(n) = n^m+ n ^m-1+...+n²+ n + c => f(n) = O(n^m)

در مثال بالا بزرگترین توان یعنی n^m میباشد پس مرتبه اجرایی آن تابع هست.

 مثال: 

f(n) =5n²- 3n +4 => f(n) = O(n²)

مثال: 

f(n) =n- 6n⁸ +n² => f(n) = O(n8)

برای مقایسه مرتبه اجرایی از مقایسه زیر استفاده کنید + مثال:

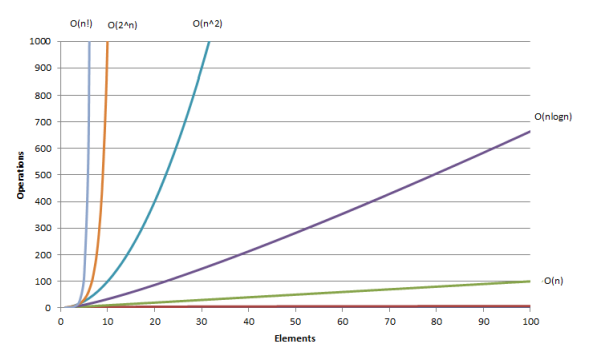
 O(1)<O(logn)<O(n)<O(nlogn)<O(n²)<O(2ⁿ)<O(n!)<O(nⁿ)

در مقایسه بالا nⁿ از همه مراتب بزرگتر میباشد.

 مثال: 

n! + 2ⁿ + 1000n¹⁰ => O(n!)

 مثال بالا را در تصویر زیر ببنید: